Menu







We understand that every student has unique needs. That's why our tutors provide personalized assistance, tailoring their approach to match your learning style and requirements.
Our team comprises scholars with extensive tutoring experience, ensuring you receive top-notch guidance.
We prioritize quality in every task we undertake. Expect well-researched, properly cited, and meticulously crafted assignments that meet your academic standards.
We cater to your individual needs, offering customized help that targets your specific academic challenges.
Deadlines are sacred to us. You can rely on us to deliver your assignments promptly, ensuring you never miss a submission deadline again.
Starting from as low as $10/page. Our services are priced competitively to ensure affordability for students on a budget.




In today’s fast-paced academic environment, students are constantly faced with the daunting challenge of balancing multiple responsibilities, from attending lectures to participating in extracurricular activities and managing personal commitments. Amidst this hustle and bustle, it’s no surprise that homework often becomes a source of stress and anxiety for many. But fear not, because AcademicPapersResearch.com is here to revolutionize the way you approach your assignments.
At AcademicPapersResearch.com, we understand the struggles that students face when it comes to homework. That’s why we’ve developed a comprehensive homework help service designed to alleviate your academic burdens and empower you to excel in your studies. With our team of experienced tutors and subject matter experts, you’ll have access to the support and guidance you need to tackle even the most challenging assignments with confidence.
So, what sets AcademicPapersResearch.com apart from other homework help services?
For starters, we prioritize quality and excellence above all else. When you choose us, you can rest assured that you’re receiving assistance from top-tier professionals who are dedicated to helping you achieve academic success. Our tutors undergo rigorous screening and training to ensure that they possess the expertise and knowledge necessary to address your specific needs effectively.
But our commitment to excellence doesn’t end there. We also understand the importance of reliability and timeliness, which is why we guarantee prompt delivery of high-quality solutions tailored to your requirements. Whether you’re grappling with complex math problems, writing an essay, or conducting research, our team is here to provide personalized assistance that meets your academic standards and exceeds your expectations.
At AcademicPapersResearch.com, we believe that accessibility is key to ensuring that every student has the opportunity to thrive academically. That’s why we offer flexible scheduling options and competitive pricing to accommodate students of all backgrounds and budgets. Whether you need help with a single assignment or ongoing support throughout the semester, we have a solution that’s right for you.
Ready to take the stress out of homework and elevate your academic performance?
Sign up for AcademicPapersResearch.com today and experience the difference for yourself. With our expert assistance and personalized support, you’ll be well on your way to mastering your assignments and achieving your academic goals. Don’t let homework hold you back any longer – let us help you unleash your full potential.
In the dynamic landscape of higher education, students are constantly navigating a myriad of challenges, from demanding coursework to extracurricular activities and personal commitments. Among these challenges, assignments often emerge as a significant source of stress and frustration, impeding students’ ability to reach their full academic potential. But fear not, because AcademicPapersResearch.com is here to revolutionize the way you approach your assignments.
At AcademicPapersResearch.com, we understand the complexities and pressures that students face when it comes to assignments. That’s why we’ve curated a comprehensive assignment help service designed to alleviate your academic burdens and propel you towards success. With our team of seasoned tutors and subject matter experts, you’ll gain access to the support and guidance necessary to conquer even the most daunting assignments with confidence.
What sets AcademicPapersResearch.com apart from other assignment help services?
Simply put, our unwavering commitment to excellence. When you choose us, you’re choosing quality, reliability, and professionalism at every step of the way. Our tutors undergo rigorous screening and training to ensure that they possess the expertise and proficiency needed to address your unique academic needs effectively.
But our dedication to excellence doesn’t stop there. We recognize that timeliness is of the essence in the academic realm, which is why we guarantee prompt delivery of meticulously crafted solutions tailored to your specifications. Whether you’re grappling with intricate mathematical problems, crafting a compelling essay, or conducting in-depth research, our team is here to provide personalized assistance that not only meets but exceeds your academic standards.
At AcademicPapersResearch.com, accessibility is at the forefront of our mission. We believe that every student deserves the opportunity to thrive academically, regardless of their background or budget. That’s why we offer flexible scheduling options and competitive pricing to ensure that our services are accessible to students from all walks of life. Whether you require assistance with a single assignment or ongoing support throughout the semester, we have a solution perfectly suited to your needs.
Ready to elevate your academic journey and unlock your full potential?
Sign up for AcademicPapersResearch.com’s assignment help service today and experience the difference for yourself. With our expert guidance and personalized support, you’ll be well-equipped to tackle any assignment that comes your way and emerge victorious. Don’t let assignments stand between you and your academic goals – let us help you pave the way to success.
At ‘academicpapersresearch.com,’ we ensure that all our tutors are thoroughly vetted and possess extensive experience in their respective academic fields. They hold advanced degrees and have a track record of helping students achieve academic success.
Our tutors offer comprehensive support, including but not limited to, explaining complex concepts, guiding you through problem-solving steps, providing feedback on drafts, and helping you prepare for exams.
We have a secure payment system in place. Once you’ve chosen a tutor and agreed upon the services, you’ll be guided through a straightforward payment process, with various options to suit your convenience.
Absolutely! You have the freedom to browse through our tutor profiles, read about their expertise, and select the one that best fits your academic needs and preferences.
Our tutors are available around the clock, so you can get help as soon as you need it. Simply submit your request, and we’ll connect you with a tutor who can assist you promptly.
Yes, we prioritize your privacy and security. All personal information is kept confidential and is not shared with third parties.
We cover a wide range of subjects, from humanities to sciences and everything in between. No matter your field of study, we have tutors who specialize in your area.
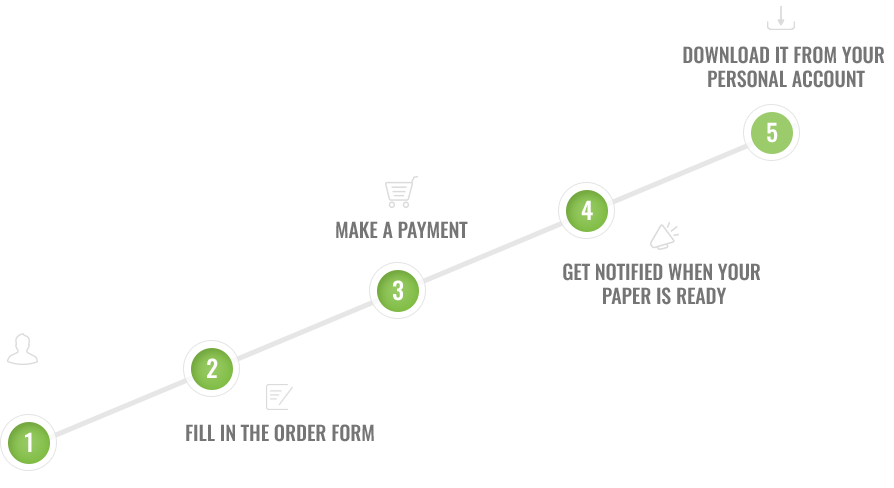
Getting started is easy. Visit ‘academicpapersresearch.com,’ sign up, and you’ll be on your way to academic support tailored to your needs.
Absolutely. At AcademicPapersResearch.com, we prioritize quality in every task we undertake. Our tutors are dedicated to delivering well-researched, accurately cited, and meticulously crafted assignments that meet the highest academic standards. You can trust us to provide top-notch assistance tailored to your specific needs.
AcademicPapersResearch.com offers a wide range of services to assist college students with their academic endeavors. These services typically include homework help, assignment assistance, essay writing, research paper guidance and writing, and exam preparation support.
Meeting deadlines is a top priority for us. We understand the importance of timely submissions, and our tutors work diligently to ensure that your assignments are completed within the agreed timeframe. You can rely on us to deliver your tasks promptly, allowing you to submit them on time without any stress.
We understand that college students are often on a tight budget. That’s why we strive to keep our services affordable without compromising on quality. Our pricing is competitive, to ensure that our services are accessible to students from all backgrounds.
Your satisfaction is our top priority. If you’re not completely satisfied with the results, we’ll work with you to make it right. Whether it’s revisions, additional assistance, or a refund, we’re committed to ensuring that you’re happy with the outcome.

How To Buy Research Papers Without Risk
Online Research Paper Writers For Hire
Research Papers For Sale: Up to 15% OFF!
Best Research Paper Writing Service Online
How to Find the Right Paper Writing Service
Expert Research Paper Help Without A Hitch
Privacy Policy • Terms of Service • Refund Policy •Sitemap
© 2003 – 2023 AcademicPapersResearch.com All Rights Reserved.